Chris and James Blog

Final Day: Today in Shanghai, noticed that…

Goodbye Shanghai. Beautiful city. Beautiful people. Sesnational maths.

Thank you to both our host schools and thank you to Maths teachers Lu and Wang who have opened our eyes to world of maths we, ourselves, were certainly never taught. As we are writing this, our bags our almost packed and our brains are almost bursting. What a privilege it’s been.

Today we’ll make this short. It’s our final day and we got to teach a lesson to Grade 5 (Year 6) maths class on Algebra. We learnt lots. We learnt that it must be incredibly difficult for EAL children to follow maths lessons and so, even more so, visual coupled with less, and only very specific, teacher talk is required; we learnt that we have learnt so much and still have so far to go; and, we learnt that the pupils in Shanghai are even faster with their number recall than even we had believed. It’s been fascinating. Our lesson today used bar models as a tool for the children to write algebraic equations correctly so that they matched worded problems. See below

By Grade 5 ( Year 6), the Shanghai teachers  would expect the children to be laying this problem out as hown below (equaltion a). This is because this calculation is a direct replica of the question. Whilst equation b will give you the correct answer it is not deemed to be correct as it does not represent the worded problem.

Today we’ll make this short. It’s our final day and we got to teach a lesson to Grade 5 (Year 6) maths class on Algebra. We learnt lots. We learnt that it must be incredibly difficult for EAL children to follow maths lessons and so, even more so, visual coupled with less, and only very specific, teacher talk is required; we learnt that we have learnt so much and still have so far to go; and, we learnt that the pupils in Shanghai are even faster with their number recall than even we had believed. It’s been fascinating. Our lesson today used bar models as a tool for the children to write algebraic equations correctly so that they matched worded problems. See below. 

Despite being slightly worried about the children being able to surpass some of what we had planned, it’s safe to say we were pleased with our lesson. We have realised that by Year 6 (Grade 5) the Chinese curriculum can become quite abstract, yet the children enjoyed the visual bar models we used to unpick the structure of worded problems. We planned our own boards and pitched a lesson based around how we would teach it in the UK. Beneath are images of the three slides that our Chinese maths counterparts particularly liked, and said they don’t really do over here.

They particularly liked our use of asking year 6 children to write their own problems based on the algebraic equations we displayed. It was mentioned to us that this was something the Chinese children did in the lower years, but not something they still do. We were actually told, in a somewhat abridged version, that the stories really helped the children understand why the formulas had to be written out in a particular way dependent upon what a word problem was asking. Whilst the problems we wrote up today were fairly complex, they were based on the similar principles that, when displayed in the bar models, 7 x 5 and 5 x 7 can look and mean different. e.g.: would you rather be paid £7 for 5 days or £5 for 7 days.

We've no doubt that it will take some time for everything to sink in. But, we do honestly believe that the visuals we've been offering our pupils, for the most part, are easily as good as what we have seen out here. What is different is that the subject knowledge of teachers, the complexity of clever questioning, the clearly thought out sequence of lessons from the textbooks and the precise focus on structure over answers is where practise in the UK appears to be lacking. With plenty to dissect and plenty of great insights and memories to bring back to our colleagues, one thing is for sure though, we are moving in the right direction in the UK and it’s something that must continue. The appreciation of just how far our practise has come really hit home today when we were in front of the class. We hadn't taught for 2 weeks, but we most certainly held our own in front of a Year 6 class whose pupils have, for almost the last decade, topped the global PISA scores by the end of KS4.

And so, with heavy hearts, we're signing off. Shanghai - it's been a blast. We hope to see you again someday. Maths teachers Lu and Wang, we look forward to seeing you soon. 

Day 8: Today in Shanghai noticed that…

It’s our second day at Minhang Experimental Primary School and our heads are still thumping! Both of us have taught Year 6, and both of us would consider ourselves fairly well versed in the curriculum. Today, however, we came up short. We have seen lessons in multiple year groups since being here in Shanghai, but the last two days in Year 6 (Grade 5) have challenged our subject knowledge more than ever. We can only hope that this blog does what we have seen today justice. Writing this without providing anyone with a presentation or slides seems almost an impossible task. In fact, I've thrown in the next pic just to show us taking some time out to practise our calligraphy – we needed it!

Right, off we go… what an amazing day it’s been. Our lead teacher literally spent hours with us unpicking distributive and associative laws and explaining to us why they teach these laws in far more depth than just a simplistic a x b = b x c or even a x b x c = c x b x a. We've gained an understanding about why children aren’t taught multiplying by fractions until secondary school over here and been blown away with the detail in which they unpick place value. To our detriment, two supposedly competent mathematicians went to an almost ‘trial-by-error’ approach to solve a Year 6 Doa No Jing problem because of our lack of multiplicative fluency (rule 3 in above table). For those of you interested, the problem is below.

0.25 x 9.2 + (        ) x (        ) = 10

We've been told, for years, that our curriculum is too broad, but the longer one spends out here, the more apparent the reason ‘why’ that is becomes evident - and we've just scrapped the surface. It's all well and good being told to slow down the learning and go into greater depth but, ultimately, you don't know what you don’t know. The intricate thought process over here in China and the subject knowledge eclipses ours. Our challenge has become how to implement things better in our schools over the next 5, 10 or even 30 year period, not just a mere year.

Yesterday, we thought that we would have delivered an algebra lesson slightly differently. We felt that the lesson lacked some visual representations, and we felt that there could have been a use of bar modelling. However, today it dawned on us as we watched the second lesson in the sequence that the reason the bar model wasn't used was that the teacher wanted a specific recording of an algebraic equation. It was explained to us that the lack of visuals now displayed were to draw out the 'correct' approach to display the mathematical equation. The teacher wanted the children to be able to write a formula that they could unpick and was so competent in his overview of the curriculum that he knew this recording of algebraic equations was essential for the pupils learning later in the year, as well as in future grades. It was also evident that the strength of the class’ mathematical fluency meant that the visuals really were not required, and when they were, they were drawn up on the boards and unpicked by the children.

The second lesson we saw today was on parallelograms and was probably the most fascinating of the day. The lesson was highly visual and led the children to making an abstract generalisation. It was the first time the children had seen the shape and the teacher provided excellent boards, practical pre-cut shapes to explore, an activity designed specifically to unpick the properties of the shape and it's commonalities with rectangles and squares. During the lesson, there was group work and paired work, as well individual time in which the children spent measuring and exploring the size and lengths of their own parallelograms.  They also finished the lesson by telling us about its relationships with ‘diamonds’… but don’t worry, that's how the word translates when referring to a Rhombus #mathsjokes. We were also told in our feedback after the lesson that the Rhombus would be introduced at this stage.

The lesson on parallelograms was meticulous – just as we’d heard it would be from some colleagues from a different hub who’d seen the lesson last week, demonstrating the incredible consistency of teaching in Shanghai. The concept was introduced to the children by reminding them about the properties of squares and rectangles, before the parallelogram was introduced. The shape was explored by the teacher who overlapped two different coloured see-through rulers. The children then saw multiple representations of different parallelograms on the board before they measured their own shapes.

They measured the lengths of the different sides, discussed whether the shape had parallel and adjacent sides, before looking at angles inside a shape and the lines of symmetry it may or may not have had.  Then children were invited to display their findings under the visualiser. All inside 35 minutes.

The great thing about this lesson on parallelograms was that there are so many elements of good teaching that we know we use already in the UK. It just seems to be a running theme that whenever we write anything about our time out here, the detail and very specific time and discussion spent unpicking concepts rises to the surface. Excited, amazed and slightly confused, we’re off to bed. See you tomorrow Shanghai!

Day 7: Today in Shanghai, noticed that…

It was another thought provoking day in Shanghai. We watched the next Grade 5 (aged 10-11) lesson in the sequence on algebraic equations and then saw a Grade 1 (aged 6-7) lesson on subtracting using partitioning. 

Again, in the Grade 5 lesson, it was clear that the teacher was able to have a really specific learning point and stick to it. The misconception he correctly anticipated was that the children wouldn’t write the conclusion to the equations that they solved. For example:

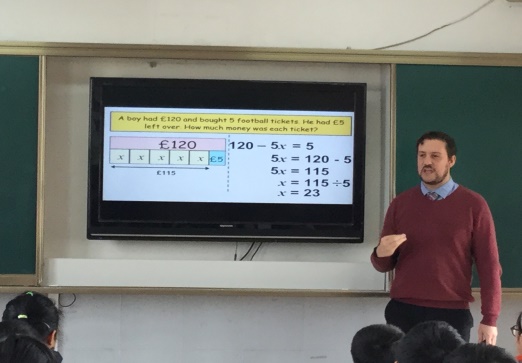
A Dad uses ¥80 to buy five children’s cinema tickets. He has ¥5 remaining. How much does one ticket cost? 

x = each child’s ticket.

¥80 – 5x = ¥5
           5x = ¥80 - ¥5
           5x = ¥75
             x = ¥75 ÷ 5
             x = ¥15

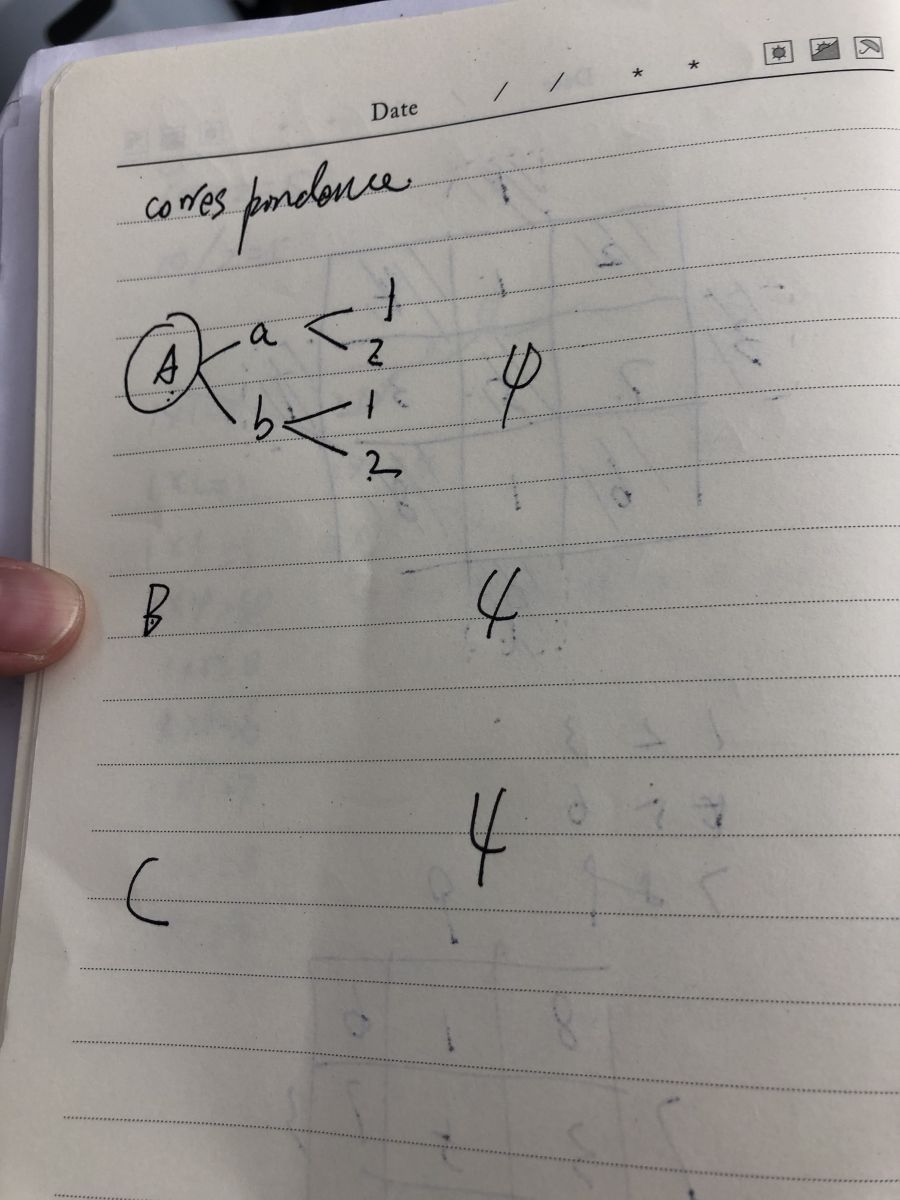
The learning he valued was the sentence at the top, which he rightly predicted would be the children’s misconception. He expertly picked apart the children’s responses, which had all correctly found that x = ¥15, under the visualiser.

X = tickets (wrong)

X = children’s tickets (wrong)

X = each child’s ticket

Again, nothing revolutionary, and something we would do - but done really clearly and precisely by ensuring that children pay attention to what the teacher wants them to so that the maths is clear. While the children have done some practise of solving equations this week, all the learning has been about giving the equation meaning.

At the end of the lesson, the learning was put into context of where it would be used in the real world - an electric bill. The maths was too complex for the children to solve but that wasn’t the point. Due to the focus that the teacher had put on writing equations in the correct order and not just the simplest to solve, they could write an equation to solve it and apply their learning. What we liked about it was that it wasn’t shoe horned into the lesson to detract from the maths, it was shown at the end to support the learning. Everything is meticulously planned out here.

The second lesson was fascinating but not for its content - which was very similar to a year 1 lesson you’d experience in the UK - but for the comparisons of the children in both countries.

Firstly, it was explained to us that Grade 1 is particularly difficult to teach in Shanghai because the gap between the most and least able children is the biggest in the school. Some children have been tutored and already know it and some are coming across it for the first time. By Grade 5, the gap is much smaller. I don’t think I can think of a more damning comparison between our two systems than that.

Secondly, at Grade 1, we saw our first behaviour chart – where the children can earn stars for their rows for good learning. The mentality is very much that the children are taught how to learn at the start of their school journey and then, supported by parental reinforcement, the responsibility to engage is on them. It is against the law to “punish” children by making them miss their play time, or stand up on a time out.

The lesson itself was well thought through, precise and packed with learning. Noticeably, having seen the world of difference between the content taught to our Year 6 and their Grade 5 this week, the content at this age was no different.

The teacher started with a problem solving task, matching up eight equations into pairs (e.g. 2+3 and 12+3) but she wasted little time in getting them to solve it. She quickly gave them the answer and drew their attention to what she wanted them to notice – 12+3 has one more ten than 2+3 – before unpicking this relationship using concrete resources.

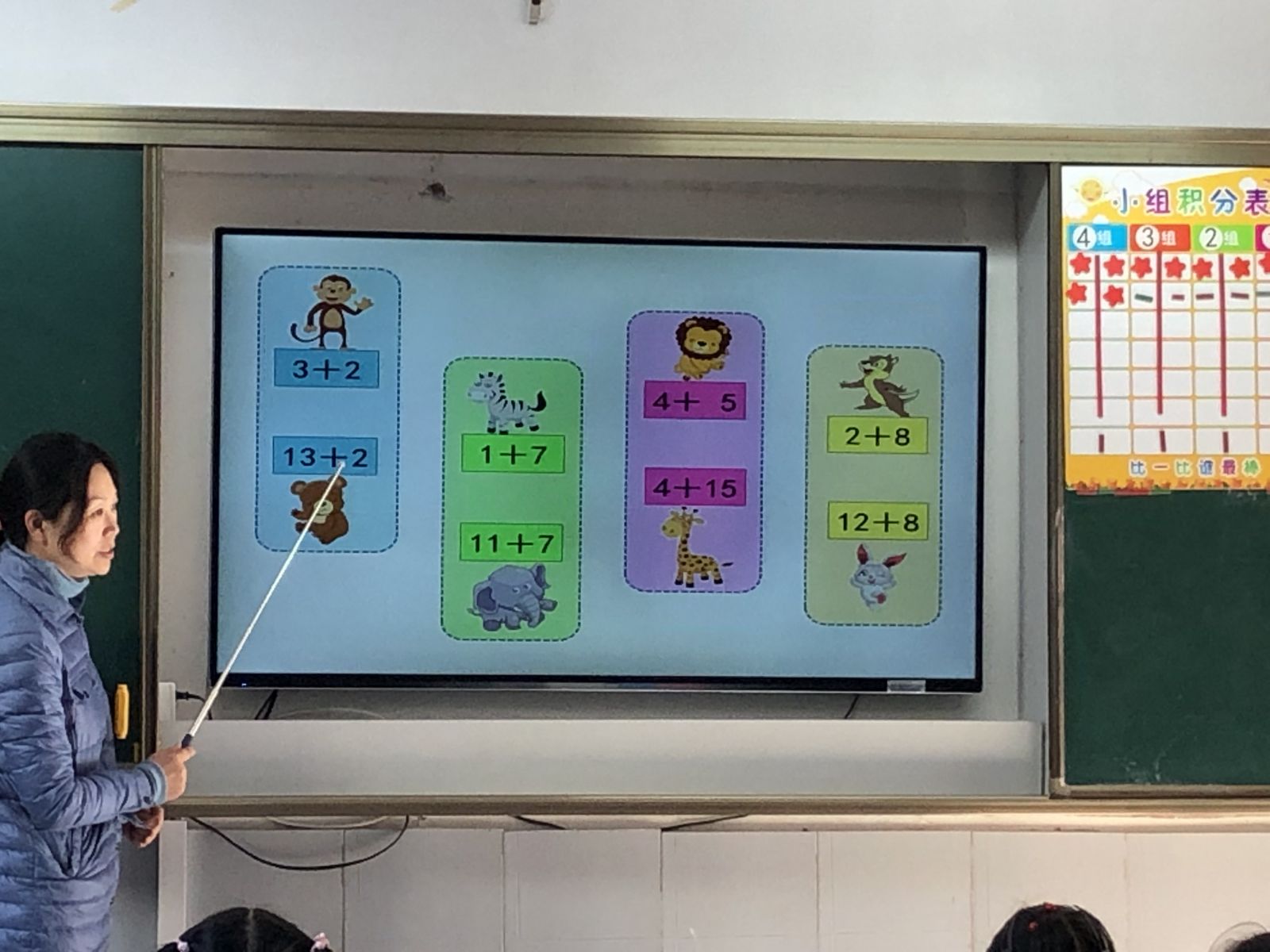
One child, who’d clearly been highly tutored, solved 12+8 by converting it to decimals but this was dismissed as irrelevant as it wasn’t the focus. When the children independently solved the equations, the focus was first on writing out the whole process before giving them a chance to solve the problems mentally.

Later on in the lesson, the teacher gave the children a chance to use the same structure of partitioning to solve subtraction equations. To further empathise the point that we’ve previously made about Shanghai teachers understanding their curriculum, our host teacher explained to us where the Year 1 sequence of lessons on subtraction fitted into supporting children with regrouping to divide in Grade 3. At their desks, today’s link from addition to subtraction was no problem for the children as the image used to support their understanding was so clear. The teacher was able to focus the discussion around why we add when we subtract using partitioning.

This leads me onto my final comparison. The fluency of the children was incredible. There were no children counting on or back as we would see in the UK. There were no children using their fingers to add. There were no children who had the barrier of not being able to add a single digit number without regrouping. The mistake they made was not to use today’s structure – the answer was easy and irrelevant.

This was the 19^th maths lesson of these children’s lives – although they would have experienced numbers at Kindergarten and at home prior to this. The first 15 lessons were all about the numbers 1-10 and they’d only been introduced to the numbers 11-20 after that. This isn’t too dissimilar to our Year 1 classrooms back home, so why are they so far ahead? The easiest answer is to bemoan the obvious barriers: additional parental support out here (or lack of for us), additional tutoring, starting school later when they’re ready to hold facts and focus longer, us having a broader and less precise curriculum etc. but a lot of those things are out of our control.

We need to think about the provision that we do offer. Our children, by the same age, would have had over fifty maths lessons of one hour, compared to 15 of 35 minutes in China, as well as our early year’s provision. How are we using this time? What can we do that we’re not doing already? We have made great strides in improving the use of resources, teaching more mathematical structures, teaching things for longer and slower, etc. but we must do more. Do our Early Years and KS1 teachers know where the maths is leading or are they rushing them towards the fastest method for SATS? Do we spend enough time on each number in EYFS? Is our EYFS environment rich enough? Do we allow the children to solve 13 + 5 by counting on when we should be forcing their attention to the structure of 10 + (3 + 2)? Can we spend more time learning number bonds to 6, to 7, to 8, etc? If we don’t teach children to be flexible with number at this age, when will they learn?

Day 6 : Today in Shanghai, noticed that…

Wow!  Today was certainly an experience! 

We arrived at our new school, Minhang Experimental Primary School, excited to see what this one had to offer. It certainly did not disappoint. The school has 6,600 children and 521 teachers, including a maths team of more than 80, split over 4 different campuses. The opportunities that the children have are incredible. We saw a TV studio for the kid’s operational TV channel, art rooms, a space emersion room, individually designed science labs, Lego rooms, music rooms, three different theatres, football pitches, a library bigger than any public one I’ve been to – and a “teacher’s library” bigger than our school library. If Chinese education does something, it wants to do it well! Last week, we were struck by the spectacular results on a broad primary curriculum of specialist teachers. Today, we saw what happens when that’s coupled with a seemingly limitless budget. 

However, the maths we observed seemed very consistent with what we witnessed last week despite an incredibly different school setting and demographic: the same text book (as is Shanghai law), similar looking classrooms and layouts, as well as similarly detailed lesson designs and reviews. The lesson we saw was observed by all seven of the other Grade 5 (aged 10/11) teachers who discussed the lesson together afterwards as part of their regular CPD.

The lesson was focussed on the children being able to write algebraic equations to represent real life problems – a concept the children struggled with. As the week progresses, the children will begin to look at learning that is above our primary curriculum. The children were learning to write the equations and why they would write them in that way but they would not be solving them problems today. Last week, the children had learnt to solve algebraic equations and this week the focus is on using them to solve real life problems. Both of us were fascinated by the lesson as we would not have spent a whole lesson on language as our teacher did today. We would have also used the bar model as a key representation and used a context to introduce the topic before solving it as a purely abstract equation. We found it confusing that there was no concrete or pictorial representation for the learning today.

These were the three questions from the text book that the lesson was designed around:

• A girl has 7 pencils. She buys some more and she now has 21 pencils. How many did she buy?

For the first question, the teacher focussed on picking out which equation best represented the problem:

21 – 7 = x, 7 + x = 21 or 21 – x = 7.

By substituting the values for words, especially paying focus to identifying what the x represented, the teacher drew out which was the correct equation. He then also discussed how to check the problem. He emphasised that you can check your answer by substituting your answer into the equation but it was also important to check the equation was right by substituting it into the word problem.

• A girl has 14 pencils. She had twice as many as another boy. How many does the boy have?

For the second problem, he looked at these equations:

14 ÷ 2 = x

14 ÷ x = 2

2x = 14

The teacher started by dismissing the first equation as the unknown was by itself. He then guided them to select the multiplication equation as it was the one that best fitted the context and when they start to use decimal numbers later in the week, they won’t be able to apply the division.

• A Grandad is 62. He is five times plus seven years older than his grandson. How old is the boy?

The third problem was one that the children have solved before using an “inverse tree” (see below). Today, he wanted to show them that putting the problem into an equation, which could then be used to solve the problem (see below).

In the TRG after the lesson, we questioned why the teacher hadn’t used a bar model and he said it was because the focus of the lesson was on unpicking the language and not using a bar model. We then shared this bar model that we might have used to expose the language:

Which could be developed to this:

The teachers liked this model and it prompted a lot of discussion – which unfortunately was mainly in Chinese and we were unable to follow it. However, they did say that they would consider using the model in the future. The constant reviews of the lessons to ensure that they are tweaked to improve year on year are a vital part of developing maths lessons in Shanghai.

On Thursday, we are due to teach a lesson. The teacher suggested that we teach the children to draw and use bar models to unpick the language so they can write an algebraic equation. This will also work as research for the Shanghai teachers as to whether the bar model is a representation that they want to use when teaching this next year.

This evening, we’ve been sat in the Sky Restaurant at the top of our hotel planning our lesson – with a little help from Claire, our secondary colleague from the South-West London Maths Hub. Our heads are certainly hurting but we’re determined to get it right and hopefully give something back to the Shanghai education system!

Day 4: Today in Shanghai, noticed that…

Goodbye Chingqing School. We look forward to greeting you on the return leg of this exchange Math Teacher Lu. Great hospitality, fantastic children and intelligent practise at its finest!!

Today was the final lesson in a sequence of lessons about measure and, like everything else in Shanghai, it did not disappoint. We had been privileged to see the two previous day’s lessons and today it was time for the children to really apply what they had learnt. Prior to today, the children had made centimetre squares, decimetre squares, stood on a metre square and today they unpicked why L x W can be used as a rule to solve the area of a rectangle. It seemed all so strange - we would have taught the children this in the first lesson AND we'd have even showed them how to work out the area of a triangle using what they'd just learnt. Wouldn't we? Well, at least we might have done some years ago. Being out here, it is certainly pleasing to see how far Maths teaching has developed in the UK in recent years, but equally it's drummed it home that we've still got a hell of way to go.

I'm sure we all, far too often, would have jumped into teaching the area of rectangle without providing the children with any real understanding of what a cm square was. Possibly, some of us might not have even known what a decimetre was, let alone a decimetre square. And, I am sure that there have been times that we have not made it explicitly obvious to the children that L x W is only ever the formula for finding the area of a rectangle. It works, of course, for a square also, but only because this is a special rectangle, and actually we can work out the area of a square by doing the side x by the side – a link that was made abundantly clear to the Chinese children. There was no stone left unturned today. It was precision at its best.

The detail and carefully planned steps across three lessons, which may have felt slow at times but had phenomenal results, meant that the children had no problem in applying their thorough knowledge to incredibly complex, abstract problems.

For example:

width = ________,

length = 6 decimetres,

area = 4,800cm

Goodbye Chingqing school and hello Minhang Experimental Primary (on Monday). The weekend is upon us and we're off to gather our thoughts while enjoying the sights of the city. Boat trips and the odd Sky Bar here we come! Not a bad weekend for a pair of primary teachers during term time. 

Day 3: Today in Shanghai, noticed that…

After being taken out for an incredible meal last night in a private room of a sky restaurant by the senior leadership team of our host school, we arrived this morning excited to observe ‘not just some lessons’, but a Shanghai style TRG.

Firstly, we couldn't help but notice that the model of CPD was phenomenal. The lesson was watched by the entire maths department and the head teacher. This is a practise that takes place on a weekly basis in every subject. Additionally, as our host school is a training school, the lesson was observed by a group of NQTs from different schools. During the TRG that followed, the NQTs sat at the side and observed our discussions. This way, they were privy to the extensive thought process and detailed discussion of the experienced teachers in breaking down the lesson. The Maths Hub has made great strides in CPD by introducing lesson studys in the UK, but this regular model of internal evaluation and development of all staff is lightyears ahead of us.

Onto the lesson…

One theme that I've noticed is that the lessons aren't a million miles away from the mastery that we have developed in England. Again, the other observation that we made yesterday in a Grade 1 lesson was that the starting point of their children is no different to ours. These children are not geniuses by genetics. So how come by Grade 2 are they so far ahead? The answer has to come in the consistency of detail and depth. The marginal gains are made through highly skilled questions and carefully-designed models constantly deepen understanding. Today's first lesson was a Grade 4/Aged 9 lesson on correspondance problems. I sat smugly in the lesson, proud that I’ve taught a very similiarly designed Year 3 lesson back in England – starting by drawing a picture of the problem, followed by drawing lines to match up the different options, before finally drawing the link to multiplication out of the children and introducing the abstract representations.

As I have back home, the teacher then used conceptual variation to represent the problem in different ways and in different contexts so the children could apply their knowledge.

However, then the magic moment came. The teacher brought up a much more complex problem using their newly aquired learning.

As they had thoroughly understood the learning, the children had no problem in finding the multiplication equation to represent the problem but there was a lack of consistency in their ability to list all of the possibilities of combinations.

This was the main criticism and discussion of the lesson from our host teacher. The children had used the equation 3x2x2 to find all of the routes from the shop to the maze. However, he felt that the problem would have more meaning for the children if they’d been exposed to and guided to use the structure 3 x (2x2) = 3 x 4 as shown below. However, the host teacher wasn’t concerned as we were observing an “inexperienced” teacher – only five years! He also linked this in to his extensive knowledge of the curriculum to tell us how the learning would develop in Grade 5, 6 and 7 and why his structure would support them further with their understanding of permutations at secondary school.

The constant requirement for and incidental use of flexibility of thinking with number is a key area where the Chinese students make accellerated progress compared to ours. Another example in the lesson was the teacher guiding the children to notice the equality of 4x4 = 3x4 + 4 and discussing which one best represented the problem.

To Chris and I, the lesson felt extremly strong. It took a concept that we felt that we’d taught well in the past and took it to a much deeper level. However, the CPD model of Shanghai meant that they will use the expertise of the school to ensure that it is taught a little stronger next time.

Day 2: Today in Shanghai, noticed that…

Another successful and eye opening day in Shanghai, not only did both James and I get the opportunity to stand up in front of a class of Chinese students (we think successfully) but we also, once again, were privileged to see the finite detail that goes into planning a lesson. Today, it was certainly the day of #resources, which were in abundance and selected deliberately to fit the purpose of the lesson.

The first lesson of the day involved us watching a Year 2 (Grade 1 Shanghai) lesson on the classification of shape.   The children were chatty, lively and talkative but ON TASK. If there are any misconceptions out there that Chinese children learn by rote, or and sit in silence, this myth was de-bunked this morning inside the first 30 seconds of the lesson. We witnessed children turning around to wave at their new English visitors, play with the bags their shapes were in and generally display all the attributes of everyday happy, enthusiastic 7 year olds. However, we also witnessed shape classification in finite detail, children engaged and eager to answer every question and a whole lot of learning.
 

Lesson 1:

Ok, so lesson 1. Every child had their own bag of  24 shapes. They had two lots (one large and one small) of four sets of shapes (circles, triangles and squares) and set about sorting them in different ways; some by shape, others by size and some colour. Like all Shanghai lessons we’ve seen so far, the lessons was so craftily planned that this was all the learning the teachers wanted the children to understand, but they unpicked it in depth. Once the children had classified their own shapes, they were directed to a set of classified shapes on display and asked to classify these further. Finally, the children were asked to play a game where they picked one of their own shapes, stood behind their chairs and remained standing if their shape contained the properties the teacher began to reveal on the board… Enter Chris and James! It was at this point we were allowed to unleash carnage upon the classroom. We think we did OK!

Lesson 2:
Once again, the use of precise resources was prevalent. The children brought their own decimetre squares to today’s class - which they had made as homework following on from yesterday’s learning. Immediately, they began by comparing the size of their decimetre squares to the size of a square centimetre, which the children had also made previously, and then to a square meter, which the teacher revealed from the inside pocket of his suit, much to the jubilation of the class. They had great fun estimating how many of which was now placed on the floor, before they got up and managed to squeeze no less than 15 of them into it. This concrete representation strengthened their ability to conceptually understand and apply in abstract equations the knowledge to convert between centimetres squared (cm2), decimetres squared (dm2) and meters squared (m2). A job well done!

After another mind blowing day at school, we look forward to being taken out for dinner tonight by our hosts.