Return leg January 2018
Our showcase events with Shangahi teachers Yi and Yiyi at The Russell School.

.jpg)
Exploring the language and structure of non-unit fractions
Our showcase events with Shangahi teachers Yi and Yiyi at The Russell School.

.jpg)
Exploring the language and structure of non-unit fractions
26/9/2017
This morning we were very fortunate to be able to observe Pen, the Maths Lead at Central no 2 School, teaching her Grade 3 (Year 4) class. Because Shanghai teachers all use the same textbook, the lesson we saw was building on a lesson we had seen Yiyi teach the week before at CGP, multiplying a two-digit number by a one-digit number. Today was focused on building understanding of the vertical method and multiplying a three-digit number by a one-digit number. It's a good thing we've come to better understand procedural variation this week because this lesson exemplified it in every way.
Pen began by displaying a set of calculations one student had prepared the day before. Another student stood and solved the calculations mentally.
3 x 7 + 3
9 x 9 + 8
4 x 7 + 5
6 + 3 x 2
8 + 6 x 4
5 + 2 x 7
Each student had prepared a set of calculations much like this in the previous lesson and now they were competing to see who could calculate the fastest. Does this seem unrelated to the lesson? Read on...
After they have warmed up with the speed challenge, all students are given the following set of calculations and are asked to solve them - through written calculations this time.
12 x 5 25 x 4 5 x 18 4 x 19
23 x 3 25 x 8 5 x 19 81 x 7
7 x 44 25 x 2 5 x 17 79 x 2
After the students have been given sufficient time to complete the task, Pen asks if they spotted any relationships which helped them to calculate more efficiently. The students respond that there wasn't a relationship in the first column, so it took the longest time. All of them also agreed that the second column was the easiest because they know 25 x 4 is 100 and they could find the other two answers by doubling and halving. Many of them said that in the third column you could calculate efficiently by adding and subtracting five from the product of 5 x 18. Finally, some said that the final column could be calculated easily through rounding, as shown below.
4 x 19 = 4 x 20 - 4
81 x 7 = 80 x 7 + 7
79 x 2 = 80 x 2 - 2
Recognise this structure? It was this very moment that Pen was preparing the students for in the introduction of her lesson. You'll notice that the number relationships get progressively more difficult to spot with each column, making the fourth column the hardest. Pen engineered this to happen in precisely this manner, but wanted to support all of her students in accessing the challenge of the final column, so she brought this structure of calculation to the forefront of their minds before presenting it. This shows layers of challenge within a single task, ensuring that students of different levels of understanding are all deepening their learning. Brilliant...
Moving into the focus of the lesson, Pen asks the students to show all of the ways they could calculate 4 x 329. All students come up with two or three options.

The first option is the most efficient. They know this method from their previous learning of two-digit by one-digit multiplication and because their understanding is deep, they know they can extend this method for use with three-digit numbers.
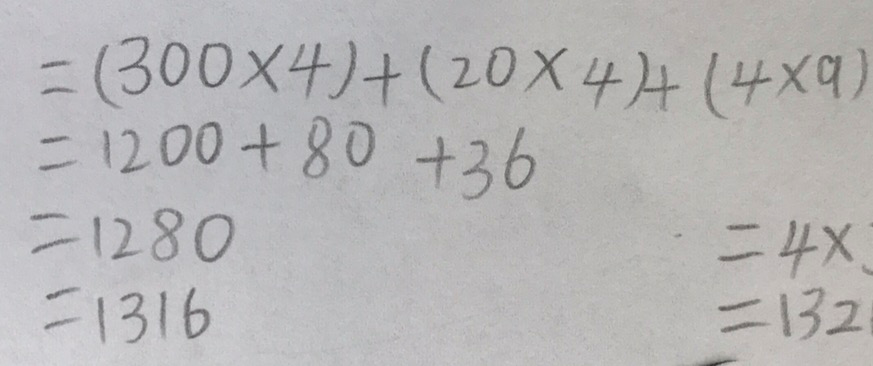
The second option shows their understanding. The vertical method is a quicker notation of what is shown here.
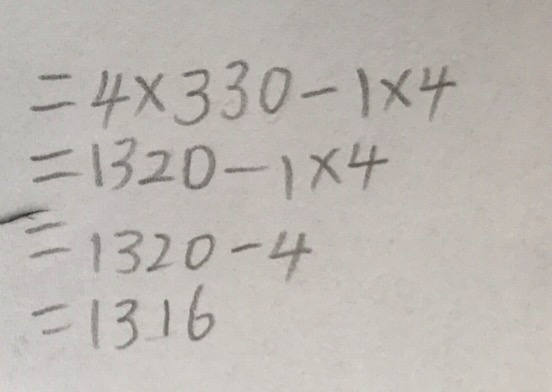
The third option links back, again, to the method of rounding and then the process of multiplying and adding or subtracting.
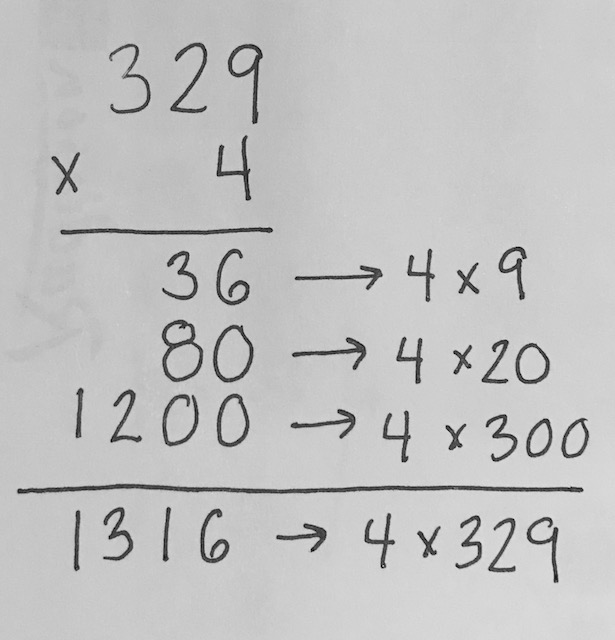
Pen looks most closely at the vertical method. She asks why we use this method (for efficiency). She asks what each step means and draws out the expanded method as the children explain. After completing her notation, she explains that what she has done is for understanding, but the shorter method that they have done is for efficiency.
They all practise this method again with three calculations: 413 x 3, 3 x 372 and 207 x 5. Note the subtle change in the position of the one-digit number from multiplier to multiplicand and back to discourage mechanical calculation. After most students have completed the calculations, Pen asks them to chant the steps together to build fluency. 3 times 2 is 6, 3 times 70 is 210, 3 times 300 is 900. 3 times 372 is 1,116.
With calculation secure, Pen moves on to a task which challenges the students to reason with their new learning.
If you multiply a three-digit number by and one-digit number (which isn't 0), how many digits will the answer be? First, make a guess (estimate) then prove it.
Students make jottings independently, then discuss options with one another. Pen required a full explanation, not just the solution. Finally, one student explains that the fewest possible digits is 3. He has proven this by multiplying the three-digit number least in value (100) with the one-digit number least in value above 0 (1). He has then extended this line of reasoning to multiply the three-digit and one-digit numbers greatest in value (9 x 999 = 8991) to prove that four is the most possible digits.
Pen takes the class one step deeper, extending the reasoning task to include 0, inspiring rich discussion amoung students and resulting in a detailed explanation of why the fewest possible digits is now one. The action on multiplying by 0 is also an important one to be introduced before the next task.
Dong Nao Jing
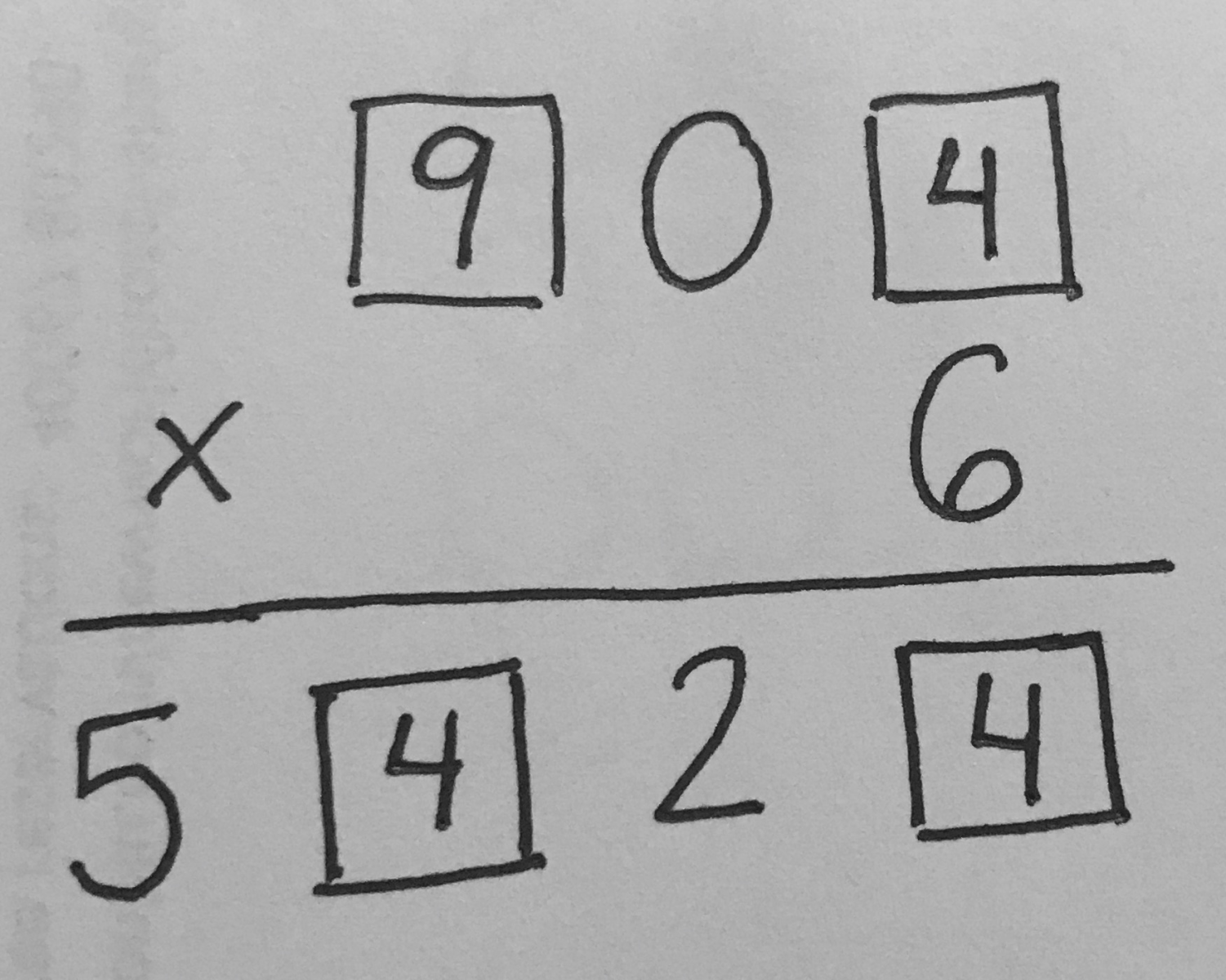
This final task can be completed two different ways, either through 'trial and error' or through reasoning. As you can imagine, the latter is the goal and it can only be accomplished if the student has studied the algorithm of the vertical method in great depth. Pen has prepared her students to be deep thinking mathematicians, so when she asks them to identify which digit is key in solving this problem, they answer '5' with confidence.
Why? Because there is only a single one-digit number that when multiplied by 6 would give you this number, and that's 9. Therefore, 9 is the missing digit in the top left.
What is the next key digit? 0 because it tells us that we would not have regrouped any digits to the hundreds column as 0 multiplied by anything is 0. This means the missing digit in the bottom left is 4 (from 6 x 9 = 54).
What is the last key digit? 2 because we know it is entirely regrouped from the ones column as the 0 would not have added any value to the tens. Therefore, the top right digit is 4 because 6 x 4 = 24, making the bottom right 4 as well.
That is certainly more than 'trial and error' - it's true understanding!
25/9/2017
This morning we headed out bright and early to our new school, Shanghai Pudong New Area No. 2 Central Primary School, where Yi Jiang has worked for the last six years. The school, built in 1889, is well established in the community and hosts 1,500 students in just one of its two campuses. Though it's the first time they've been involved in the England-Shanghai exchange, they are committed to international outreach and collaboration and have developed ongoing partnerships with schools in Finland and America in the past few years alone.
After our tour of this lovely school, we headed to our first observation, taught by Yi to her Grade 2 (Year 3) class. To introduce the lesson, one of Yi's students stood at the front of the class and lead them in singing their five times tables song. In the summer before Grade 2, the students are instructed to memorise their times tables songs from 1 to 9. This means that when they arrive back after the holidays, they will be prepared to build their understanding of multiplication without having to simultaneously memorise facts. To some, this may seem backwards. Should you not first understand and then build fluency? In Shanghai, they consider the times tables to be extremely important and they believe that by first memorising these facts, the mind is freed to deepen understanding without distraction. They also believe that memorisation is best done at home as time at school with the specialist Maths teacher is better spent exploring more complex learning.
Once the class has completed their song, Yi tells a story. There are a group of animals having a race. The frog is small, but his strong legs allow him to jump 5 paces with only one hop. After 3 hops, he has travelled 15 paces (using the answer as a starting point). This is depicted on the whiteboard as a number line.
How does this relate to the times tables?
In our song, five times three is fifteen and three times five is also fifteen.
Yi presents two number sentences (5 x 3 = 15 and 3 x 5 = 15) and asks the children what they mean. These children have not yet encountered multiplicative notation, but they can relate it to the words they know from the song (making connections from known facts to new understanding). They repeat a stem sentence.
The frog hops 3 times and each hop passes 5 paces. He travels 15 paces in total. 3 times 5 is equal to 15.
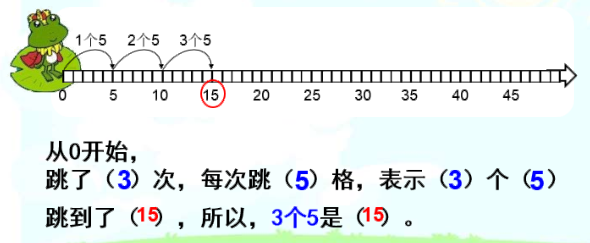
Yi then asks students to suggest another amount of hops the frog might take. For each, they reveal the related number sentences and repeat the stem sentence. With each suggestion, Yi puts the two number sentences on the board, listing them in order and leaving spaces where some are missing.
2 x 5 = 10 5 x 2 = 10
3 x 5 = 15 5 x 3 = 15
-
-
6 x 5 = 30 5 x 6 = 30
-
-
9 x 5 = 45 5 x 9 = 45
After listing a few possibilities, Yi tells the students to look at the sentences listed and suggest the missing options in ascending order. They start with 1 x 5 / 5 x 1 then 4 x 5 / 5 x 4 and so on, working strategically.
Once the list is complete, they look at all of the number sentences and try to spot patterns.
They all include the number 5.
The multiplicand/multiplier increases by one each time.
The product increases by five each time.
The sentences with an even multiplicand/multiplier have a product with a ones value of 0.
The sentences with an odd multiplicand/multiplier have a product with a ones value of 5.

24/9/2017
This morning we met in the hotel for a lecture on variation from Debbie Morgan and Huang Xingfeng and a special lesson study prepared by ten of our Chinese partner teachers, including Yiyi Chen.
First, Debbie reviewed the lecture we had received on our first day from Professor Wu regarding the history and application of conceptual and procedural variation. She reiterated that models of conceptual variation could be classified as standard, non-standard and non-concept. The first classification, 'standard', being the classic representation, such as a regular pentagon. The second, 'non-standard', being an unexpected or less recognisable example, such as an irregular pentagon. The last, 'non-concept', would be an example which does not fit the criteria of the concept but treads very close to it, such as a quadrilateral. Each classification should be present in all lessons as they support students in developing a deep understanding of the essential criteria which defines a concept, how to identify it in unfamiliar contexts and how to spot the differences from other near-concepts.
The understanding of procedural variation was the real takeaway today. For both of us, this has been a sticking point throughout our involvement with the Hub for nearly two years. It has been the hardest to grasp and has yet seemed to be the most impactful element in the Teaching for Mastery approach. I'm happy to say that today was the light bulb moment!
Debbie defined procedural variation as building the concept in a progressive manner through the small, logical steps taken within the lesson (from simplicity to depth). Each step connects with the one before it and the one following it so that children's understanding is built from what they know already to the deep appreciation of a new concept.
Professor Xingfeng gave the example of multiplying 12 x 23. First, we would began with the students' knowledge of single-digit times tables and their relation to multiplying two-digit numbers where the ones value is 0 (i.e. 3 x 7 = 21; 30 x 7 = 210; 30 x 70 = 2,100) . Next, we would move on to introducing the distributive law to build understanding [12 x (20 + 3) and (10 + 2) x 23 and (10 + 2) x (20 + 3)]. Eventually, we would arrive at the most efficient algorithm, the vertical method (or column method). It is very important that we do not start with this algorithm, but rather build on known facts and take slow connected steps, finally landing on the new concept. In this case, were we to start by teaching the vertical method, we would simply be teaching a procedure. This kind of surface understanding is easily misunderstood, forgotten or can become unrecognisable to students when placed in a different context.
After hearing from Debbie and Huang, we were given our lesson on 'subtraction through decomposition' which was aimed at Grade 2 (Year 3) students.
The first slide asked us to recognise a number presented on a double tens frame.

13.
How do you know?
Because the first tens frame is full and the second has three counters.
The second slide asked us to identify another number, this time with two incomplete tens frames.
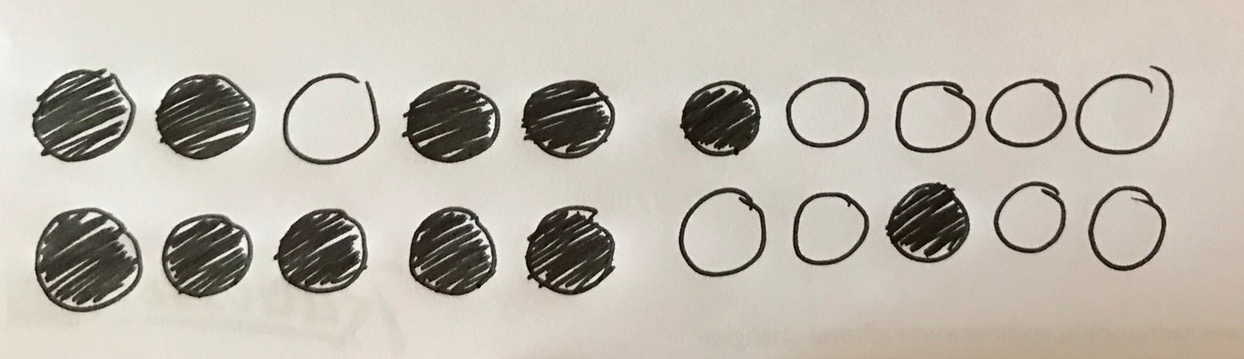
...11.
How do you know?
Because if I move one counter from the second frame to the first, then the first will be complete and there is only one left in the second.
Why did recognising the number on this slide take longer than the last?
Because there were more steps in the process so it was less efficient.
This activity reinforced what we, the students, knew about the power of ten. A deep understanding of ten and how other numbers relate to it is fundamental in one's ability to reason with number. It is also the essential first step from which we will build our understanding of a new concept in this lesson.
Next, our teacher presents us with the calculation 14 - 5 and asks us to use our tens frame to solve the problem.
How did you solve the calculation?
I subtracted 4, which brought me to 10 and then I subtracted 1 which brought me to 9. (Ah, the power of ten!)
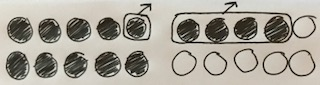
Is there another method?
Using my counters, I removed 5 from the complete tens frame then I added the remaining 5 to the 4 on the other tens frame, resulting in 9.
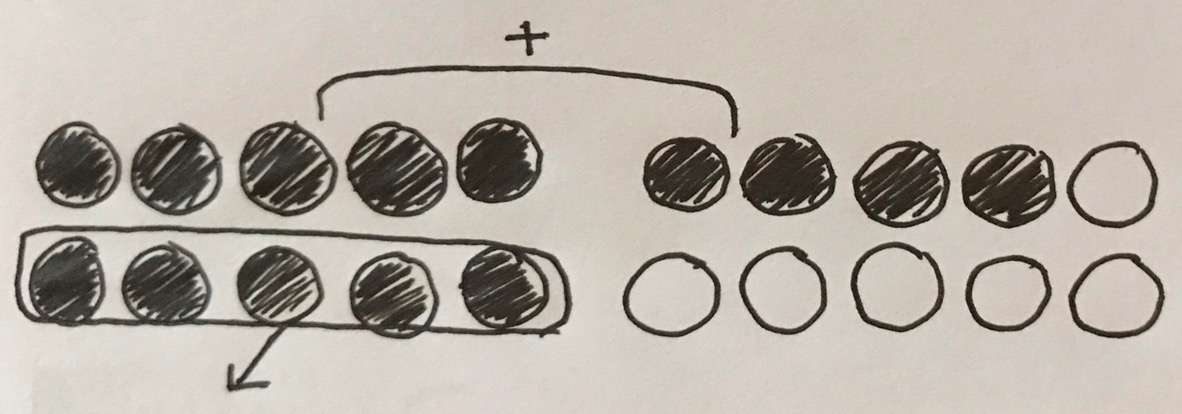
Can either of these methods be represented on a number line?
The first method (called Down over Ten - or bridging ten, in the UK) is easily represented on a number line, but the second method (Subtract from Ten) does not seem logical in a linear representation.
Our teacher now presents us with a new calculation, 16 - 9. This very carefully chosen question cleverly directs us towards using the Subtract from Ten method (partition 10 into 9 and 1, then add 1 to 6), though Down Over Ten works as well (partition 9 into 6 and 3, then subtract 3 from 10). We discuss the methods. What do they look like on a double tens frame? How can we describe them in a sentence? What does the notation look like? Which is more efficient here? Why?
Eventually, we are fluent using these two methods. It doesn't matter that we've only use two calculations. Our understanding is secure and so we are ready to recognise these concepts in a new environment. Our teacher has prepared a set of cards on each table. Some are number sentences, some are notations of the Down Over Ten Method and others of the Subtract From Ten method. We are instructed to 'make friends' - to group the method notations with their corresponding number sentences. Rich discussion follows as some number sentences have one friend (either Down Over Ten or Subtract From Ten) while others have two (both methods) and sadly, some don't have any at all - but we write some method notations down for those so they aren't lonely! We examine the matches, deciding which friends are better suited (which method is more appropriate for each number sentence) and why that might be. Our teacher also presents a non-concept example by suggesting that two methods which come to the same result should be matched as friends.
13 - 5 = 8
13 - 3 = 10
10 - 2 = 8 (Down Over Ten)
and
16 - 8 = 8
10 - 8 = 2
2 + 6 = 8 (Subtract From Ten)
These calculations, however, do not match because the number sentences are different and they are also geared towards different methods.
The intention of this lesson is to understand and compare these two methods so that later students may develop their use of Down Over Ten for quick mental calculations and the use of Subtract From Ten in the vertical method of subtraction (when exchanging). It takes us from the known (the power of ten) through small connected steps, eventually arriving at the ability to recognise the connection of two different calculation methods and their matching number sentences. Variation - ta dahh!
Those of you familiar with the 5 Big Ideas may be asking, "Hey - isn't this just Coherence?" Yes. It most certainly is. Others still might be asking, "Isn't questioning to expose connections the goal of Mathematical Thinking?" Absolutely, it is! The 5 Big ideas are a brilliant way to organise in our minds the immense amount of pedagocial theory involved in TfM but we cannot think of them as completely separate entities. Fluency is achieved through Mathematical Thinking which is built around Representation & Structure which is exposed through the use of Variation and it is all communicated through Coherence. These ideas are interconnected and work together to build deep mathematical understanding in our students.
23/09/2017
Eager not to waste a moment of our time in this incredible city, we woke up early and were out the door by 8:30am. Yiyi, Yi, Chen and Silia had very generously organised a trip to Zhujiajiao, one of the oldest water cities in Shanghai. The city dates back 1,700 years and has built up and evolved over time, always centered around the canal. Upon entering through the arched gateway, we boarded a man-powered boat similar to a gondola and travelled along the narrow canal which was framed with small shops and food stalls selling a range of options including beef wrapped in bamboo leaves, the specialty dish of Zhujiajiao.

We continued on down the channel, eventually crossing a larger waterway and finally coming to a stop just past the temple.
It was the first time to the city for all of us, including our hosts, so we just enjoyed wandering around, checking out the local handicraft and crossing back and forth over some of the many bridges, of which there are thirty-six built in different styles and materials. The largest and most famous of these bridges is Fangsheng Bridge, or the 'setting the fish free bridge', where locals come to release fish into the water for good luck.

In the evening, we joined again for a meal of 'huoguo', or hot pot. This dish is known to many in the UK, but the experience in Shanghai was one entirely of its own. We each ordered a broth base, which was brought to the table and set upon individual burners. While waiting for the broth to boil, we headed over to the sauces table where we created our very own mixture from the sixteen flavours available. Back at the table, we filled our broth with the selection of vegetables, meat and tofu which was regularly replenished by passing waiters. Feeling full to the brim and delightfully satisfied, we headed back to the hotel, agreeing that the incredible food and wonderful company had resulted in our best meal yet!


22/09/2017
We were treated to a very special welcome this morning as the Primary Lead of the NCETM, Debbie Morgan, was joining us for the day. Upon entering the lobby, music began and two traditional Chinese dragons (manned by four very talented students) marched forward and began to dance and greet each other. Next, a group of eight girls wearing blue tutus and bow ties entered from 'side stage' and performed a routine which they'd clearly worked to perfect over many practices. What an incredible way to start the day and close our time at CGB! After pictures and exchanges of gratitude, we headed up to observe Chen for the final time before her trip to London in November.
Today's lesson built on the concept of the part-whole relationship that we'd seen introduced earlier in the week. Following that exploration, it was time to focus on defining a unit fraction, relating it to real experiences and exploring the meaning of the abstract representation. Chen began by reviewing the concept of equal parts by dividing by two.
We know that 4 lollies divided equally between 2 people is 2.
We also know that 2 apples divided equally between 2 people is 1.
But how do we divide 1 cake between 2 people?
Children readily answer that each person will receive half of the cake, but their understanding of 'half' is from personal experiences only and has not yet been linked to a mathematical definition or representation. Chen presents the abstract symbol of 1/2. She draws the vinculum (fraction line) first: this means 'divided into equal parts'. Next comes the denominator: this tells us how many equal parts exist. Last, she writes the numerator: this tells us how many of the equal parts are shown. The process of writing the fraction in this order, a standard practice in China, gives the children a far greater understanding of the representation, and even the concept of a fraction.
1. The parts must be equal (vinculum).
2. There are a set number of equal parts (denominator).
3. We are considering a number of those parts (numerator).
At this point, Chen introduces the stem sentence. "When we divide a cake into two equal parts, each part is 1/2 of the cake." The children then experiment further with the concept of half by folding cutouts of hearts and triangles (slightly non-standard representations) and using the stem sentence to describe their findings.
The challenge deepens. Now there are four children and they would all like some cake. Chen reveals an image of the cake being cut into four pieces of varying sizes - a classic non-example to emphasize the importance of dividing into equal parts! This is not fair. The parts must be equal so that each child receives the same amount of cake. We repeat the stem sentence again in this new scenario.
After further exploring 1/4 through folding squares, Chen presents 1/5 to the children as an abstract representation (using the answer as a starting point). She shows three images to the students and asks them to judge whether or not they show 1/5. The first example challenges the notion of equal parts: there are five parts and one is shaded but it does not show 1/5 because the parts are not equal. The next example is correct, and the students explain how it fits all the necessary criteria. The last example is important because it exemplifies another common misconception - the confusion between proportion and ratio. Because 1 part is shaded and 5 parts are not, children might feel that the numbers 1 and 5 should be used as numerator and denominator. However, the denominator is the sum of all of the parts, so in fact, this image shows 1/6.
At this point, Chen has introduced problems visually (images of lollies, apples and cakes), through concrete resources (folding paper) and through abstract representations (1/5). Next, she removes even more support by asking aloud, with no slide to support her question, "Now that we have seen 1/2, 1/4, 1/5 and 1/6, can you imagine how to write the fraction if we divide a whole into 8 equal parts? 9 equal parts? 12 equal parts?" It is clear through the students' responses that they were developing a deep understanding of the features of a fraction and the importance of its abstract representation. These were not the all-too-familiar one-word answers, these were full explanations with reasoning scaffolded through the use of the stem sentence.
In the afternoon, we were invited to join the special Art lesson that students were given on Friday afternoons. Five classes running along the corridor each engaged in five different activities with a focus on traditional Chinese art styles. One group tied knots with ribbon around bunched silk scarfs, then dyed sections with different colours, creating a tie-dye pattern. The next class rolled, shaped and carved clay, recreating a well-known butterfly sculpture. Another group created traditional costume designs using ornate and patterened origami paper. The following group traced and copied porcelain patterns onto bookmarks, fans, pencil cases and even transparent mobile phone cases. The last class traced and cut out the silhouette of ancient pottery and then added detailed designs to their cut-outs.
It was wonderful to see these children relaxing and enjoying a relatively unstructured afternoon, but upon reflection, they were just as engaged as we had always seen them. At CGP, the development of the whole child is paramount, be it through practising mindfulness during focused art experiences, encouraging creativity through their special Odyssey of the Mind course or engaging in Maths lessons with small key learning points which allow children to deepen understanding, explore their misconceptions and embed learning for life-long understanding.
21/09/2017
This morning we observed a rather unexpected sort of Maths lesson. Another teacher at the school, Teng, was kind enough to invite us to her Grade 5 (Year 6) lesson which used the Long March, an important historical event in China, as a means of exploring large numbers. For those who are unfamiliar, the Long March was a retreat of the Chinese Communist Party from Jiangxi province of southern China to the northern mountain region of Shanxi. The CCP was unable to travel north directly as they would encounter their opposition, the Nationalist Party, so instead they travelled a circuitous and treacherous route. This event is very important and well known to the Chinese - and its tale also happens to include many large numbers.
After watching a quick video clip, recalling the events of the Long March, Teng presented the students with some numbers: the length of the Jangtze River (6,300 km); the length of the Great Wall (6,700 km); and the length of the Long March, as estimated at the time of the march (25,000 li / 12,500 km). The children discussed these numbers. They knew from having visited or studying maps that the wall and river were very long, which meant that the Long March must have been extremely long.
Next, Teng presented another set of numbers: a 5km race; a marathon (42.195 km); and the approximate circumference of Earth (40,000 km). Once again, the students were asked to compare the numbers to the length of the Long March. At first, these numbers seemed unrelated and random. From an outsider's perspective, it wasn't clear how this fit into what we define as a Shanghai style of teaching. Then the students shared their conclusions.
"If I run 5 km each day, it would take me approximately 7 years to complete the Long March."
"I would have to run approximately 300 marathons!"
"The distance covered is approximately one third of the Earth's circumference!"
Ah - now it's clear! Students, and people in general, have trouble understanding the true scale of large numbers. 10,000 is a lot. 100,000 is A LOT. 1,000,000 is A REALLY BIG LOT! But what are these numbers really? What is the experience of 'a lot'?
Teng had identified this difficulty in her students' perception of large numbers. They could calculate effortlessly with great accuracy, which they demonstrated many times over in the lesson, but they didn't have personal experience of the scale of large numbers. They hadn't walked the 12,500 km of the Long March, so how could they truly appreciate the magnitude? The answer is to find connections between these large numbers and the experience of smaller numbers.
5 km is not very long, but it does take quite a bit of effort to run. Imagine running that distance every day for 7 years! You would certainly cover a great distance!
Though the Shanghai curriculum is heavily structured with the use of standardised textbooks, through intelligent practice, Teng decided this concept was important enough that she must to go off-script.
What a wonderful way to learn about an important event in China's history while developing one's abilties to appreciate magnitude.
Thank you, Teng!
In the afternoon, we were able to observe our partner teacher Yiyi Chen once again with her Grade 3 (Year 4) class. In addition to the national curriculum, each school in Shanghai offers special classes which are specially designed to reflect the values of that particular school. One of these classes at Cao Guangbiao P.S. is 'Maths Activities'. This is held at a different time from the other Maths lessons as it does not follow the sequence of learning.
The lesson began with a countdown. 3...2...1... a six-digit number appears on the board. The class goes completely silent, eyes fixed ahead and not a hint of movement. A short moment later, the board goes blank and the children drop their heads and start writing furiously. Before some have finished, the countdown has begun again. 3...2...1... a seven-digit number with one digit missing. 3...2...1... an eight-digit number. 3...2...1... a nine-digit number! After much buzz and excitement over who managed to remember the coveted nine-digit number, it was time to move on to the next activity - 'Make 24'.
5 5 9 9 appeared on the board. Being fans of the show 'Countdown', we quickly discovered what was happening. The children had to use the four digits, along with any of the four operations, to arrive at 24. I'm only slightly embarrassed to report that these eight-year-olds put us to shame with their speed and accuracy. This is yet another example of how fundamental times tables and number bonds are to our engagement in Maths. At least we matched the students in our unfettered enthusiasm.
The purpose of 'Maths Activities' is singular - let children have fun playing with Maths. How lovely! In the UK, it is not uncommon to hear children, parents and even teachers expressing that they don't like Maths, they're no good at Maths, Maths is boring to them. It seems that there is a real place in our society for dedicating some time to developing our love and enjoyment of such a critical discipline.
20/09/2017
Today we returned to Cao Guangbiao P.S. to learn from some more brilliant Maths teaching. The first lesson we observed, taught by our partner teacher Yiyi Chen, focused on multiplying a two-digit number by a one-digit number. The lesson began with a set of twelve calculations, including 100 x 4, 300 x 6, 30 x 7 and 30 x 70. Though at first glace, these may seem to exceed the objective of the lesson, in fact, they only require knowledge of single-digit times tables and a secure understanding of place value. After giving the students a chance to complete the calculations, Yiyi asked them to explain their methods, highlighting key concepts that would be used later in the lesson.
Next, Yiyi presented a problem. One box contains 12 packets of crisps. If each box costs 42 yuan, how much would three boxes cost? Already, students are confronted with dong nao jin (simply put, the requirement 'to use one's mind'). How do we solve this problem? What information do we have? Is any of the information presented superfluous? Yes. The fact that each box contains 12 packets of crisps is not needed to solve this problem. It has been intentionally included as a distraction. Can you imagine a more impactful way to prepare students for solving problems in the real world, where they are confronted with an overload of information and must decide for themselves what is relevant and what is not? These students, clearly practised in the art of 'using one's mind', immediately overlooked the '12' and sought to solve the calculation of 3 x 42.
The remainder of the lesson focused on looking at the partitioning method, expanded method and vertical method. Students experimented with the three, discovering that though they all come up with the same result, the vertical method is the most efficient. Through comparing these three models, they were able to give meaning to the highly abstract and short-hand vertical method, deepening their understanding beyond that of a procedural interpretation.
.png)
The lesson closed with a final calculation, a preview of tomorrow's learning point: 23 x 4. It's at this point that we discover the brilliance of this lesson. Throughout, it felt simple and effortless (from a teaching perspective). Actually, it was meticulously designed and each calculation was carefully considered. 23 x 4, though seemingly fitting within the context, is unique. 3 x 4 = 12. Now, we have a digit in the tens column before even multiplying the tens. This is an entirely new and different skill, and in line with the Shanghai approach of taking microscopic steps, it is a concept that must be addressed in its very own lesson. Nice one, Yiyi!
After our inspiring morning, Yiyi, Chen and Yi took us to the striking Buddhist Jing'an Temple on West Nanjing Road. Originally built in 1216, the traditional building contrasts beautifully with the modern skyscrapers that have been built up around it in the development of present-day Shanghai. Worshippers gathered in the centre courtyard to burn incense and bow towards the cardinal directions before visiting the four temples which housed impressive Buddhas, including a 3.8 meter jade Buddha, the largest of its kind in the country. Not even the torrential rain, which persisted through the afternoon, could take away from the grandness of this impressive temple and pagoda, hidden in the centre of the most populous city in the world.
.png)
19/09/2017
Today we delved into the real purpose of out visit - to observe and learn from our Shanghai counterparts. We travelled the lengthy 3 minute walk from our hotel to Cao Guangbiao Primary School to observe Chen Chen teaching a lesson focused on the Part-Whole relationship as a precusor to fractions. We found the lesson to be overflowing with expert delivery of the Shanghai pedagogy we've come to know through our Teaching for Mastery journeys. The steps were small and carefully considered, as the learning point was very targeted and key to the conceptual understanding of proportion. Stem sentences were used fluidly through the lesson to consolidate learning and ensure involvement of all students.
Chen Chen guided the students in exploring the common misconception that a 'whole' must always be a 'whole' and can never be a 'part' when, in fact, Shanghai is a part of China but China is a part of the world. With this, the children were able to deepen their understanding by reasoning that ‘part’ and ‘whole’ are defined by their context.
.jpg)
Examples and non-examples were highlighted in true or flase scenarios which had been carefully prepared to expose the structure of this concept. For example, is half an apple a part? No, it is not. A part cannot exist unless it relates to a whole. So, half an apple is only a part when one apple is the whole. You can imagine the rich discussion that resulted from this debate!
This afternoon we had the opportunity to analyse some of the Shanghai textbooks from Grade 1 and 2 and are hoping to explore their use of variation and representation more this week.
.jpg)
18/9/2017
Today the real experience began as we ventured to Shanghai Normal University for the launch day of the England-Shanghai Mathematics Teacher Exchange Project. Representatives from the English and Chinese departments of education warmly welcomed all of the teachers and Professor Gu Lingyuan provided an in-depth lecture on the finer points of variation.
After lunch, we finally had the chance to meet with our partner teachers for the duration of the project. It came as no surprise that Yi Jiang and Yiyi Chen are very passionate Maths teachers, keen to share their practices and grow as professionals. We shared ideas about Math pedagogy,discovered the similarities and differences of our two education systems and began thinking ahead to their visit to England in January.
To close the evening, our hosts warmly invited us to a traditional Shanghainese meal in the city.
17/9/2017
We've arrived!
After a ten-hour extended movie night at 30,000 feet, we finally landed in beautiful Shanghai. Though we were part of a very slow moving bunch, looking a bit worse for wear, everyone was keen not to waste the day - especially as we have a jam-packed schedule ahead!
After checking into our lovely hotel, we headed out to Nanjing Road to see the shops, taste some of the local confectionery (some sort of tasty rice cubes) and travel along to the historic Bund to take in the views of modern Shanghai.